[hackeroid] B1:5 Tamed Dragon

If you have felt our analogy with dragon very well, you could get an impression that The Dragon listens to you very easy and quickly after studying simplified algoritms of Tamed Dragon, as if it became the pet. But attention! As soon as you go out of the house (of number systems with bases of 2, 8 or 16), you again must tame it and withstand its attacks.

Algorithms of Tamed Dragon are based on two Dragon Tables, large and small one. Here they are:

   +------+---+----+      +-----+---+
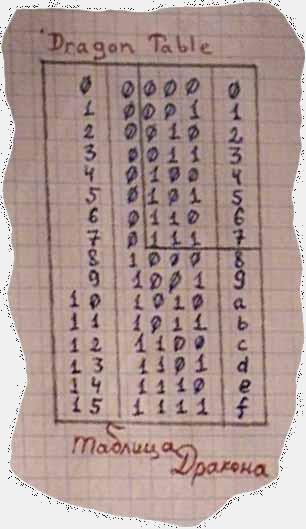   | 0000 | 0 |  0 |      | 000 | 0 |
   | 0001 | 1 |  1 |      | 001 | 1 |
   | 0010 | 2 |  2 |      | 010 | 2 |
   | 0011 | 3 |  3 |      | 011 | 3 |
   | 0100 | 4 |  4 |      | 100 | 4 |
   | 0101 | 5 |  5 |      | 101 | 5 |
   | 0110 | 6 |  6 |      | 110 | 6 |
   | 0111 | 7 |  7 |      | 111 | 7 |
   | 1000 | 8 |  8 |      +-----+---+
   | 1001 | 9 |  9 | Small Table of Dragon
   | 1010 | A | 10 |
   | 1011 | B | 11 |
   | 1100 | C | 12 |
   | 1101 | D | 13 |
   | 1110 | E | 14 |
   | 1111 | F | 15 |
   +------+---+----+
Large Table of Dragon

When we draw them on paper we usally select in Large Table part which is the same as the Small one and get two tables in one. Large Table of Dragon would be useful while working with hexadecimal machines of IBM PC kind, Small one -- while working with octal machines, like BK series.

This tables pop up so often in hacker's life, from such non-linked places, that you will have to learn it by heart. I have used a couple of paperbooks in small script, always restoring them by heart till I remembered them. I would advice you not to repeat this, but learn it now -- the will be very useful. :-)

The main usage of Dragon Tables is conversion between hexadecimal number system and binary one (Large Dragon Table) and between octal and binary ones (Small Table Of Dragon).

As you know, there are similar languages. For example, ancient slavic and russian, russian and ukrainian. While usually you have to look up in the dictionary the whole word, during translation from ukrainian to russian it is enough to know the table of relations between letters. For example, to change letter 'i' to '¨', and '¨' to 'ë' in its turn.

Binary and hexadecimal, binary and octal number systems play the role of such similar languages. And The Dragon Table is the conversion table. So let us walk thru all the cases. Watch out, there are stones underwater.

16->2

This is simple. Four binary digits (bits, bit=Binary digiT) relate to hexadecimal number according to Large Dragon Table. After the conversion of whole number one has to cross out leading zeroes, if any.

12FC_16 = 0001 0010 1111 1100_2 = 1001011111100_2

2->16

Slightly harder. The sequence of bits is divided into groups of four from the right, and if the last group misses some zeroes, it will be padded with them.

1011001011_2 = 0010 1100 1011_2 = 2CB_16

8<->2

Conversions between binary and octal number systems are very similar except for using the Small Dragon Table and dividing binary number into groups of three bits.

276_8 = 010 111 110_2 = 10111110_2
1011001011_2 = 001 011 001 011_2 = 1313_8

WARNING! Algorithms of Tamed Dragon exist only for conversions 16<->2 and 8<->2. To convert 16<->8 one should use temporary binary number system. Using algorightm of Tamed Dragon for conversion to decimal number system or from it is the excessive error. You will be disqualified at attestation.

Please remember the formula of Simplified Dragon: 8<->2<->16.

WARNING! Common mistake!

Every hacker has the period in his life when he suddenly by some unexplainable reason starts to think that numbers in which no letters are used do not change during conversion to decimal number system. I.e. for example 123_16=123_10. IT IS WRONG! Think why. Calculate what 123_16 is equal to using Taming Algorithm.

>>>

It is often needed to convert bytes and words from binary system to decimal. Instead of long and boring calculations using the Taming Algorithm one can quickly convert the number into hexadecimal number system and then -- to decimal. A lot of time is being saved.

1010 1001_2 = A9_16 = 10*16+9 = 169_10

Byte is being converted at the moment and in mind.

<<<

<<<B1:5 EOF>>>


E-mail: hscool@netclub.ru
Hosted by uCoz