B1:5 Ручной Дракон.

Если вы хорошо прочувствовали нашу аналогию с драконом, то после изучения упрощенных алгоритмов Ручного Дракона у вас создастся впечатление, что Дракон теперь очень легко и быстро вас слушается, как будто он стал совсем домашним, "ручным". Но внимание! Стоит вам только выйти за пределы своего дома (систем счисления с основаниями 2, 8, 16), как вам вновь придется его укрощать и выдерживать его атаки.

Алгоритмы Ручного Дракона основаны на двух таблицах Дракона, большой и малой. Вот они:

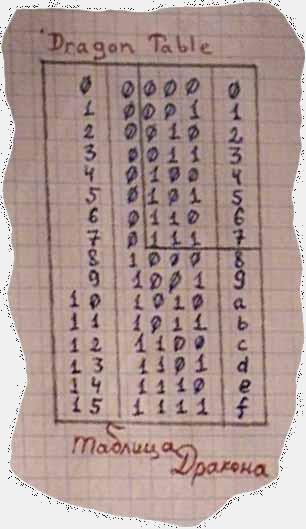+------+---+----+ +-----+---+ | 0000 | 0 | 0 | | 000 | 0 | | 0001 | 1 | 1 | | 001 | 1 | | 0010 | 2 | 2 | | 010 | 2 | | 0011 | 3 | 3 | | 011 | 3 | | 0100 | 4 | 4 | | 100 | 4 | | 0101 | 5 | 5 | | 101 | 5 | | 0110 | 6 | 6 | | 110 | 6 | | 0111 | 7 | 7 | | 111 | 7 | | 1000 | 8 | 8 | +-----+---+ | 1001 | 9 | 9 | Малая таблица Дракона | 1010 | A | 10 | | 1011 | B | 11 | | 1100 | C | 12 | | 1101 | D | 13 | | 1110 | E | 14 | | 1111 | F | 15 | +------+---+----+ Большая таблица Дракона

Когда мы рисуем их на бумаге, мы обычно отчеркиваем в Большой таблице Дракона ту часть, которая совпадает с Малой и получаем две таблицы в одной. Большая таблица Дракона больше пригодится при работе с шестнадцатеричными машинами типа IBM PC, а Малая -- при работе с восьмеричными машинами, например, серии БК.

Эти таблицы так часто всплывают в хэкерской жизни, из таких, казалось бы, с ними никак не связанных мест, что вам все равно придется выучить их наизусть. Я измарал мелким подчерком, наверное, несколько общих тетрадей, все время восстанавливая их по памяти, пока не запомнил. Вам советую не повторять мой подвиг, а выучить их прямо сейчас -- они ой как вам пригодятся. :-)

Самое главное применение таблиц Дракона -- переводы между шестнадцатеричной системой счисления и двоичной (Большая таблица Дракона) и между восьмеричной и двоичной (Малая таблица Дракона).

Как известно, существуют родственные языки. Например, древнеславянский и русский, русский и украинский. Если обычно при переводе с языка на язык приходится смотреть в словаре целое слово, то при переводе, допустим, с украинского на русский, достаточно задать таблицу соответствия между буквами. Например, менять букву 'i' на 'и', а 'и', в свою очередь, на 'ы'.

Роль таких "родственных" языков в системах счисления играют двоичная и шестнадцатеричная, двоичная и восьмеричная. А таблицей перевода и являются таблицы Дракона. Итак, разберем все случаи. Следите за нами, здесь есть подводные камни!

Ну это просто. Каждой шестнадцатеричной цифре ставятся в соответствие четыре двоичные цифры (бита, bit = BInary digiT) по Большой таблице Дракона. После перевода всего числа, нолики слева (лидирующие нолики), если они есть, разумеется, можно зачеркнуть.

Немногим сложнее. Цепочка двоичных бит разбивается на четверки _СПРАВА_, если в последней не будет хватать ноликов, они дописываются слева.

Переводы между двоичной и восьмеричной системами очень похожи, только используется Малая таблица Дракона и разбивка двоичного числа на тройки битов.

276_8 = 010 111 110_2 = 10111110_2
1011001011_2 = 001 011 001 011_2 = 1313_8

ВНИМАНИЕ! Алгоритмы Упрощенного Дракона существуют лишь для переводов 16<->2 и 8<->2. Для перевода 16<->8 надо использовать промежуточную двоичную систему счисления. Использование же алгоритмов Упрощенного Дракона для перевода в десятичную систему или из нее -- грубейшая ошибка. За нее вы будете выгнаны с аттестации коленкой под зад!

Вообще, запомните формулу Упрощенного Дракона: 8<->2<->16.

ВНИМАНИЕ! Распространенное заблуждение!

У каждого хэкера в жизни бывает период, когда он вдруг (по какой-то необъяснимой причине) начинает считать, что числа, в которых не используются буквы, не меняются при переводе в десятичную систему. То есть, например, 123_16=123_10. Так вот, ЭТО НЕ ТАК! Подумайте, почему. Посчитайте, чему равно 123_16 по алгоритму Укрощения.

>>>

Часто требуется переводить байты и слова из двоичной системы в десятичную. Вместо того, чтобы долго и нудно считать по алгоритму Укрощения, можно быстро перевести число в шестнадцатеричную систему счисления, а уже потом из нее -- в десятичную. Экономится куча времени.

1010 1001_2 = A9_16 = 10*16+9 = 169_10

Байт переводится мгновенно и в уме!

<<<

<<<B1:5 EOF>>>

• Back to: BASE, hscool ONLINE, hscool, REMOTE

: hscool@netclub.ru